Как зарегистрироваться и пройти Первую математическую олимпиаду Школково

Первая математическая олимпиада Школково — это ежегодное интеллектуальное соревнование для школьников младших и средних классов. Главная цель проекта — заинтересовать детей математикой, научить их нестандартно мыслить и показать, что решение задач может быть увлекательным процессом.

В отличие от многих других конкурсов, здесь акцент сделан не на проверке школьной программы, а на умении рассуждать. Задания построены так, чтобы участник смог проявить находчивость и логику. Это делает олимпиаду доступной для ребят с разным уровнем подготовки и превращает участие в увлекательное приключение. Она рассчитана на учащихся 4–7 классов.

Регистрация и правила участия

Чтобы попасть на олимпиаду, необходимо пройти регистрацию на сайте https://3.shkolkovo.online/matholymp. Организаторы открыли её заранее, но она может быть закрыта за несколько дней до начала в случае набора участников. Процесс максимально простой: указываются данные ребёнка, класс обучения и контактный email.

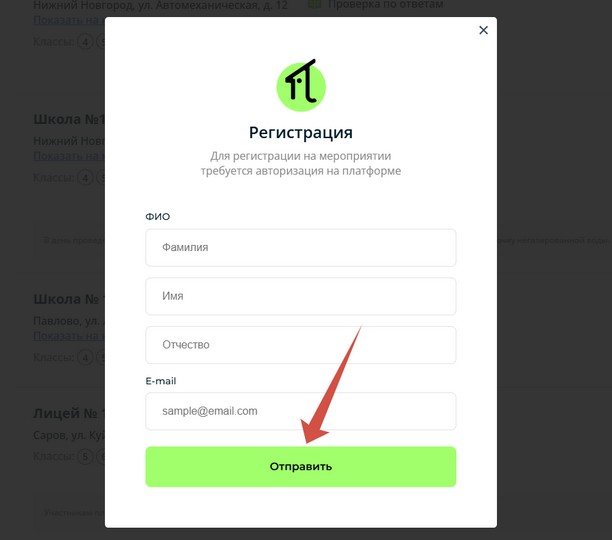
При очном формате школьнику потребуется прийти на площадку 21 сентября 2025 года. С собой берут ручку, карандаш и документ, подтверждающий личность или школьную принадлежность.

Продолжительность олимпиады составляет около 90 минут. За это время школьнику нужно решить набор задач, количество которых зависит от класса и уровня сложности. После завершения работы бланки или онлайн-формы отправляются организаторам для проверки.

Результаты публикуются через несколько дней. Все участники получают электронные сертификаты, а победители и призёры — дипломы. Этот формат мотивирует детей и позволяет каждому почувствовать значимость собственного участия.

Задания и примеры задач

Главный интерес олимпиады — это задания. Они не похожи на стандартные школьные упражнения и требуют гибкого мышления. Среди типичных направлений:

• Комбинаторика в упрощённой форме;
• Логические задачи на внимание;
• Арифметические ребусы и хитрые вычисления;
• Элементарная геометрия с нестандартными условиями.

Пример условной задачи: «У Маши есть 10 карандашей пяти разных цветов. Каждый цвет встречается хотя бы дважды. Может ли она выбрать три карандаша так, чтобы среди них было два одного цвета?»

На первый взгляд задача простая, но она проверяет умение рассуждать и использовать принцип Дирихле. Именно такие задания формируют логическую культуру и готовят к более серьёзным олимпиадам.

На доске написано 10 чисел. За один ход разрешается стереть любые два числа и вместо них написать их разность по модулю. Докажите, что в конце на доске останется число, кратное 2.

В задаче используется принцип инварианта: чётность чисел сохраняется. Сколько бы раз мы ни брали разности, хотя бы одно чётное число останется до конца.

Пять лягушек сидят на кочках в ряд. Каждая может прыгать только на соседнюю кочку. Возможно ли переставить лягушек так, чтобы они полностью поменялись местами?

Секрет в том, что перестановка возможна, но требует длинной последовательности ходов. Задача проверяет умение мыслить пошагово и строить стратегию.

В коробке лежат 30 конфет: 12 карамелек, 10 шоколадных и 8 ирисок. Сколько конфет нужно взять, чтобы гарантированно оказалось хотя бы 5 одного вида?

По принципу Дирихле, если взять 12 конфет, можно получить по 4 каждого вида. Следующая, 13-я, гарантирует 5 конфет одного типа.

Разбирая подобные примеры, ребёнок учится находить ключевую идею и объяснять решение пошагово. Это полезно не только для математики, но и для развития аналитического мышления в целом.

Как готовиться к олимпиаде

Подготовка к олимпиаде Школково не требует углублённых знаний, но системность важна. Условно процесс можно разделить на три этапа:

1. Изучение базы задач. Начните с решения архивных заданий прошлых лет. Это поможет понять стиль формулировок и уровень сложности.
2. Тренировка с таймером. Олимпиада длится полтора часа, и этого времени хватает только при правильном распределении. Регулярные тренировки с отсчётом времени учат концентрироваться и решать задачи в заданный срок.
3. Повторение приёмов. Стоит выделить ключевые методы: перебор, логические рассуждения, построение вспомогательных фигур, использование инвариантов. Освоение этих приёмов делает задачу менее пугающей и помогает быстрее находить решение.

Родителям и педагогам важно помнить: ребёнок должен идти на олимпиаду с настроем на интересный опыт, а не только на победу. Это снижает стресс и делает участие радостным событием.

Чем отличается Первая олимпиада Школково от других

Первая математическая олимпиада Школково выделяется доступностью и дружелюбным форматом. Она рассчитана на школьников, которые только делают первые шаги в олимпиадном движении. В отличие от крупных всероссийских конкурсов, здесь нет сложных теоретических задач или громоздких доказательств. Всё построено так, чтобы ребёнок сам захотел продолжать заниматься математикой. Кроме того, у участников есть возможность познакомиться с курсами и тренингами, которые помогают углубить знания. Многие школьники, начавшие с Первой олимпиады, позже успешно выступают на региональных и всероссийских соревнованиях.

Подготовка с помощью курсов и самостоятельных занятий

Школково предлагает собственные курсы для подготовки к олимпиадам. На них разбираются типовые задачи, формируются навыки рассуждений и даются методические подсказки. Такой вариант подойдёт для тех, кто хочет системности и поддержки преподавателя.

Тем, кто готовится самостоятельно, стоит составить план. Например:

• Раз в неделю решать 5–7 задач;
• Раз в две недели устраивать тренировку «под олимпиаду» с таймером;
• Разбирать ошибки и искать альтернативные решения.

Главное — регулярность. Даже один час в неделю, но стабильно, принесёт больше пользы, чем интенсивные, но редкие занятия.

Психологический аспект участия

Для ребёнка олимпиада — это не только математика, но и эмоциональный опыт. Атмосфера нового события, ожидание результатов, общение с другими участниками — всё это формирует уверенность в себе.

Родителям важно поддерживать ребёнка и акцентировать внимание на процессе, а не только на дипломах. Даже если результат окажется скромным, опыт участия даст уверенность и интерес к будущим соревнованиям.

Учителям, сопровождающим школьников, стоит объяснять детям, что каждый участник уже победитель, потому что решился попробовать силы и получил новый опыт.